Question

I'm very confused on what to do :/

Answer 1

To simplify a term under a square root, we are going to try and find factors of the term that are to a power of 2. This is because when there is a term under a square root that is being squared, the powers cancel out and we are left with the term itself. An example of this is:

`√(8x^4) = √(2^2 \cdot 2 \cdot x^2 \cdot x^2) = 2x^2√(2)`

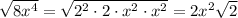
So, we will first look at the 99. Are there any factors of 99 that are a whole number squared? Sure! 9 is equal to
`3^2`. Thus, we can say that 99 simplifies as follows:

`99 = 11 \cdot 3^2`

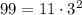
(Remember that the 11 comes from the fact that 11 times 9 is equal to 99. We can't have a 3^2 without the 11!)

Now, let's look at the
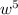`w^5`. Remember that exponents of the same base add to each other. Thus, we can say:

`w^5 = w^2 \cdot w^2 \cdot w`

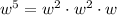
Now, let's examine the
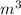`m^3`. Again, using the fact that exponents add, we can say:

`m^3 = m \cdot m^2`

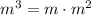
Now, let's substitute all of this back under the square root to get:

`√((11 \cdot 3^2) \cdot (w^2 \cdot w^2 \cdot w) \cdot (m^2 \cdot m))`

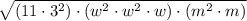
The next step is to take out the terms to the power of 2. This gets us:

`3 \cdot w \cdot w \cdot m √(11 \cdot w \cdot m)`

`3w^2 m √(11wm)`

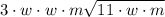
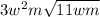
Our answer is
`\boxed{3w^2 m √(11wm)}`.

Answer 2

`√(99w^5m^3)`

`√(99) √(w^5m^3)`

`√(99)=3√(11)`

`=3√(11)√(w^5m^3)`

Hope this helps!

Thanks!

-Charlie