If
 is an even function, then
is an even function, then
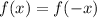 . In this case,
. In this case,
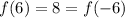 .
.
This is because an even function is symmetric about the
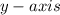 . Hence the outputs of a negative x-value and a positive x-value are the same.
. Hence the outputs of a negative x-value and a positive x-value are the same.
The correct option is the first option.
Since the graph is even, the outputs of a negative x-value and a positive x-value are the same.