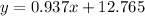Question

Find the least squares regression equation using the school year (in number of years after 2000) for the input variable and the average cost (in thousands of dollars) for the output variable. (Hint: USE DESMOS)

(SHOW WORK)

Answer 1

The least squares regression equation using the school year (in number of years after 2000) for the input variable and the average cost (in thousands of dollars) for the output variable is "y=0.937x+12.765" .

Solution-

The independent variable / input variable= x = Number of years after 2000 ( = year-2000)

The dependent variable / output variable = y = Average cost in thousands of dollars

(The table has been attached herewith.)

To find the regression equation for a group of (x,y) points,

We have to calculate the slope and y-intercept, then we can put those values in the equation y = mx + c ( Slope - Intercept formula)

We know that,

`Slope=m=(N\sum xy -\sum x\sum y)/(N\sum x^(2)- (\sum x)^(2))`

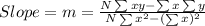
Putting the values from the table,

`m=((8 * 1020.206)-(52 * 150.894))/((8 * 3810)-(52^2))`

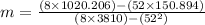
( ∵ Instead of 150,894 we have to put 150.894 as we have find the line for year and thousands of dollars )

`\Rightarrow m =(8161.648-7846.488)/(3040-2704) =(315.16)/(336)=0.937`

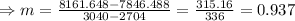
Now, for the y-intercept,

`c =(\sum y -m(\sum x))/(N)`

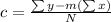
Putting the values,

`c=(150.894-(52 * 0.937))/(8)=(102.125)/(8)=12.765`

Now, putting the values of c and m, in the Slope-Intercept formula,

`y=0.937x+12.765`