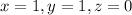Question

Solve the system by elimination.

-2x + 2y + 3z = 0
-2x - y + z = -3
2x + 3y + 3z = 5

(please sow your work)

Answer 1

These are three linear equations in in three variables.



`- 2x + 2y + 3z = 0 - - (1)`


`- 2x - y + z = - 3 - - (2)`

`2x + 3y + 3z = 5 - - (3)`

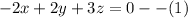
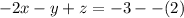
To solve this by elimination, we are going to add equation (3) to (1) and (2) simultaneously.


First equation (3) + (1)

This implies that


`0+ 5y + 6z = 5`

`5y + 6z = 5 - - (4)`
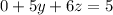
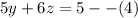
Next let's add equation (2) and (3)

This implies that


`2y+5z=2--(5)`

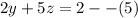
Equations (4) and (5) are simultaneous linear equation in two variables.


Equation (4) ×2


This implies that



`10y + 6z = 10 - - -(6)`
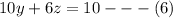
Also equation (5) ×5


This implies that


`10y + 25z = 10 - - - (7)`
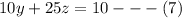
Now equation (7) - (6) gives


`13z = 0`

`\rightarrow \: z = 0`
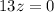
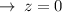
Substitute

`z = 0`
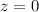
in equations (6) or (7) and solve for y.

So using equation (6),

`10y + 6(0) = 10`

`10y + 0 = 10`

`10y = 10`

`\therefore \: y = 1`


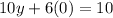
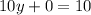
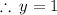
Now plug in z=0 and y=1 into (3) or any other containing the three variables and solve for x.



`2x + 3(1) + 3(0) = 5`

`2x + 3 + 0 = 5`

`2x = 2`

`x = 1`

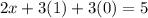
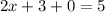
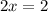
Hence


`x=1, y= 1, z=0`