Question

1)Which system of linear inequalities is graphed?

A){x<−2y≤−x−1
B){x<−3y≤−x+1
C){x≤−3y≤−x−3
D){x<−3y≤−x−1

2)Which system of linear inequalities is graphed?

A) {y≤2x+1x+y≥−2
B) {y≥2x+1x+y≤−2
C) {y<2x+1x+y>−2
D) {y>2x+1x+y<−2

Answer 1

Answer: C and B

Explanation:

Answer 2

1 ) D

2 ) D

Explanation:

The general form of the straight line is given by y=mx+c, where m is the slope and c is y-intercept.

1 ) According to the graph, we get the co-ordinates (0,-1) and (-1,0).

Using these so-ordinates, we will find the equation of the line.

i.e. Slope
`m = (y_(2)-y_(1))/(x_(2)-x_(1))`

i.e.
`m = (0-(-1))/(-1-0)`

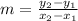
i.e. m = -1

Now, substituting m and (0,-1) in general form, we get c = -1.

So, the equation of this straight line is y = -x-1.

We will now use 'Zero Test' i.e. substitute (0,0) in the required equation and since the given regions are away from the origin, this pair of points will not satisfy the equation.

So, we get y < -x-1 and as the region is given to less than x= -3.

Hence, option D is correct.

2) Now, according to the second graph, we get the points (0,-2), (-2,0) and (0,1), (-1,-1) for two lines respectively.

Solving as in 1) we get that the equations of the lines are given by x+y = -2 and y = 2x+1 respectively.

Again using 'Zero Test', we see that these pair of points does not satisfy the equations.

So, we get x+y < -2 and y > 2x+1.

Hence, option D is correct.