Question

An average mosquito found in the environment gives of 12.6 disintigrations per minute per gram of carbon. a preserved mosquito found inside of an amber fossil found in the new england states gives off 1.575 disintigrations per minute per gram of carbon. with a half life of 5,730 years for carbon 14 how old is the mosquito roughly? answers are in years, you do not need to include the word years though in the answer

Answer 1

From the half life equation, the remaining fraction
`((1)/(2) )^{(t)/(T) }`

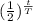
where t = total time elapsed and T = Half life

Now, it is given that,
`T=5730`

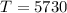
And remaining fraction is
`=(1.575)/(12.6)`

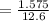
So, substituting these values in the above equation,

`(1.575)/(12.6)=((1)/(2) )^{(t)/(5730) }\\0.125=0.5^{(t)/(5730)`

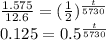
Taking log both sides,

`log(0.125)=log(0.5)*(t)/(5730)`

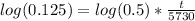
Solving, we obtain that,

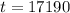`t=17190` years