Question

To hang lights up on his house.Garrett place is a 14 foot ladder 4 feet from the base of the house. How high up the house will the ladder reach

Answer 1

Answer: 13.42 feet

Explanation:

Given : To hang lights up on his house.Garrett place is a 14 foot ladder 4 feet from the base of the house.

Since house is standing vertical to to ground making a right angles , so the triangle made by ladder must be a right triangle, where ladder is a hypotenuse.

Let h be the height of the house where the ladder reach.

By Pythagoras Theorem , we have

`x^2+4^2=14^2\\\\\Rightarrow\ x^2+16=196\\\\\Rightarrow\ x^2=196-16\\\\\Rightarrow\ x^2 =180\\\\\Rightarrow\ x=√(180)=13.416407865\approx13.42\text{ feet}`

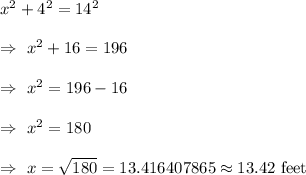
Hence, the height of the house where the ladder reach= 13.42 feet

Answer 2

This seems like a right triangle problem.

So assuming 14 feet is the hypotenuse and 4 feet is a leg of the right triangle, we can use the pythagorean theorem (
`a^(2) +b^(2) =c^(2)`) to solve for the height of the house, in which we shall name it x.

So, the equation is
`4^(2) +x^(2) =14^(2)`.

Solve for x:

16+x^{2}= 196

x^{2}= 196-16

x^{2}= 180

x = 6√5 feet

Hope this helps!