The probability that a randomly selected customer takes more than 10 minutes will be 8.38%
Step-by-step explanation
The average or mean
 is 8.56 minutes and standard deviation
is 8.56 minutes and standard deviation
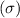 is 1.04 minutes.
is 1.04 minutes.
Formula for finding the z-score is:
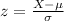
So, the z-score for
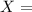 10 minutes will be.....
10 minutes will be.....
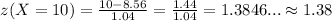
Now, according to the standard normal distribution table,
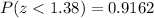 . So.....
. So.....
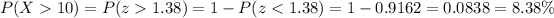
So, the probability that a randomly selected customer takes more than 10 minutes will be 8.38%