Answer:
Part 1:
we have to find the value of x
we have been given the lines f and g are parallel
Interior angles on the same side are supplementary.
Hence, the two given angles will be equal to 180
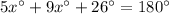
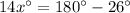
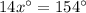
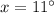
Therefore, Option B is correct.
Part 2:
We have to find x
l and m are parallel
Two parallel lines are cut by Transverse line
And angles on the opposite sides that are alternate interior angles are equal
Hence,
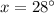
Therefore, option A is correct.
Part 3:
a. m∠5=

and m∠2=
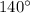
b. m∠5+m∠2=
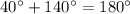
c.∠5 and ∠2 are supplementary because they are
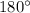
d.∠5 and ∠2 are same side interior angles since, they are
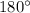
e. a || b since, a is
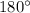 and b is also
and b is also
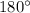 .
.