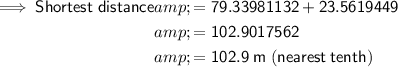Question

Answer this question please very important
will give loads of points

Answer 1

102.9 m

Explanation:

The shortest distance from A to C would be diagonally from A to C.

This comprises:

• Two straight paths of equal length (shown in blue on the attached diagram).
• Half the circumference of the central circle (shown in red on the attached diagram).

The length of the diagonal between A and C can be calculated using Pythagoras Theorem:

`\begin{aligned}c^2&=a^2+b^2\\\implies \sf AC^2 & = \sf AB^2+AD^2\\\sf AC^2 & = \sf 50^2+80^2\\\sf AC^2 & = \sf 2500+6400^2\\\sf AC^2 & = \sf 8900\\\sf AC & = √(\sf 8900)\\\sf AC & = \sf 94.33981132\;m\end{aligned}`

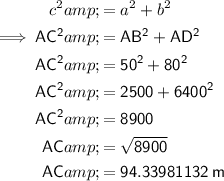
Subtract the diameter of the circular path from this to calculate the sum of the lengths of the straight paths.

`\implies \sf 94.33981132-15=79.33981132\;m`

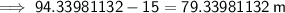
To calculate the length of the circular part of the path, find half the circumference of the central circle:

`\begin{aligned}\implies \textsf{Half the circumference} & = \sf (1)/(2) \pi d\\& =\sf (1)/(2) \pi (15)\\& =\sf 23.5619449\;m\end{aligned}`

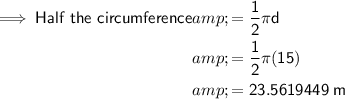
Therefore, the shortest distance from A to C across the park is:

`\begin{aligned} \implies \textsf{Shortest distance} & = \sf 79.33981132+23.5619449\\& = \sf 102.9017562\\& = \sf 102.9\;m\;(nearest\:tenth)\end{aligned}`