Question

Solve the system. If there's no unique solution, label the system as either dependent or inconsistent.

2x + y + 3z = 12
x – y + 4z = 5
–4x + 4y – 4z = –20

A. Dependent system (infinite number of solutions)
B. Inconsistent system (no solution)
C. (4, 1, 2)
D. (1, 4, 2)

Answer 1

Neither c or d are correct for the entire system so it has to be B. A is not possible because we have already proved two solutions to be incorrect

Answer 2

The solution of the equations are

`x=(17)/(3),y=(2)/(3)\texttt{ and }z=0`

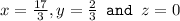
So all the options are wrong.

Explanation:

We have

2x + y + 3z = 12 -------------------eqn 1

x – y + 4z = 5 -------------------eqn 2

–4x + 4y – 4z = –20 -------------------eqn 3

eqn 2 x 2

2x – 2y + 8z = 10 -------------------eqn 4

eqn 4 - eqn 1

2x – 2y + 8z - (2x + y + 3z) = 10 - 12

-3y +5z = -2 -------------------eqn 5

eqn 1 x 2

4x + 2y + 6z = 24 -------------------eqn 6

eqn 3 + eqn 6

–4x + 4y – 4z + 4x + 2y + 6z = -20 + 24

6y + 2 z = 4 -------------------eqn 7

eqn 5 x 2

-6y +10z = -4 -------------------eqn 8

eqn 7 + eqn 8

12 z = 0

z = 0

Substituting in eqn 7

6y + 0 = 4

`y=(2)/(3)`

Substituting in eqn 2

`x-(2)/(3)+4* 0=5\\x=(17)/(3)`

So the solution of the equations are

`x=(17)/(3),y=(2)/(3)\texttt{ and }z=0`

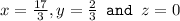
So all the options are wrong.