These are three simultaneous linear equations in three variables. The idea is to reduce these equations to two simultaneous linear equations in two variables and finally to a linear equation in one variable.
We can then solve the linear equation in one variable, and get the remaining variables by backward substitution.
The first equation is
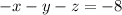
Multiplying through by negative one we obtain,
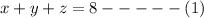
The second equation is

The third equation is
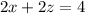
Dividing through by 2 , we obtain;
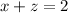
Making z the subject, we get;

Now we substitute equation (3) into equation (1) and (2) simultaneously.
Equation (3) in (1) gives,
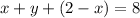
This implies that,
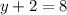
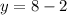
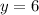
Now equation (3) in (2) gives,

Expanding the bracket gives,
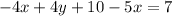
Grouping like terms and simplifying gives,
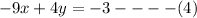
Put
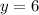
in equation (4).
This implies that,
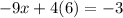
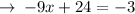

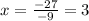
We now put
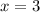
in equation (3) to obtain,


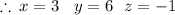
In general, if you are solving three linear equations in three variables:
1. Make one variable the subject in one of the equations, preferably the simplest or easiest equation
2. Substitute this equation into the other two equations.
3. Solve the two simultaneous equations in two variables