Question

(Please give a numerical answer, 50 points) A projectile launcher is placed on the floor and pointed straight up (90 degrees), The projectile (ball) leaves the launcher 27 cm above the floor. The ball has a mass of 6.58 g. We measure the maximum height above the floor reached by the ball. We do this three times and get the following results all measured in meters.: 2.32, 2.26 and 2.37. Find the speed at which the ball leaves the launcher.

Answer 1

Speed at which the ball leaves the launcher = 6.34 m/s

Step-by-step explanation:

The readings of height above the floor reached by the ball = 2.32, 2.26 and 2.37

Mean value
`=(2.32+2.26+2.37)/(3) =2.317 m`

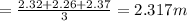
Initial height of launcher = 27 cm = 0.27 cm

So maximum height of projection = 2.317-0.27 = 2.047 meter

We have equation of motion,
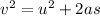`v^2=u^2+2as`, where u is the initial velocity, v is the final velocity, s is the displacement and a is the acceleration.

In this case we need to consider only vertical factors.

Vertical displacement = 2.047 m, acceleration = acceleration due to gravity =
`-9.81m/s^2`, final velocity = 0 m/s, we need to calculate initial velocity.

`0^2=u^2-2*9.81*2.047\\ \\ u=√(2*9.81*2.047) \\ \\ u=6.34 m/s`

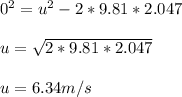
So, speed at which the ball leaves the launcher = 6.34 m/s