Question

A recipe for beef stew calls for 1 pound of beef and 3 potatoes. The recipe is doubled to include 2 pounds of beef and 6 potatoes. Which propitiation represents the situation?

Answer 1

b and d

Explanation:

Answer 2

To answer the question, let B call the amount of meat and P the number of potatoes.

The recipe says that for every pound of meat we need 3 potatoes.

Then that relationship is written as follows:

`1B = 3P`

`(1)/(3)=(P)/(B)`

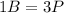
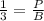
If we increase the amounts of the recipe by 100%, it will multiply by 2 the amount of meat and also that of potatoes. Therefore we need 2 pounds of meat and 6 potatoes.

Then the relationship is:

`2B = 6P`

`(2)/(6)=(P)/(B)`

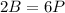
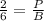
But
`(2)/(6)=(1)/(3)`

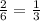
Therefore, the proportion that represents the situation remains the same
`1B = 3P`

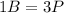
This occurs because the increase in the amount of potatoes and beef was in the same proportion.