Question

I need help with questions 4 and 5 on the math homework

Answer 1

Question 4

Recall the following facts:


1. If two lines are parallel, their slopes are the same

2. If two lines are perpendicular, the product of their slopes equals 1.

The line given to us is:


`y = (3)/(4) x + 12`
By comparing to ;


`y = mx + c`

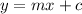
The slope is

`m = (3)/(4)`
Now let us compare this to:


`y = (4)/(3) x - 2`
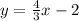
which has slope

`= (4)/(3)`
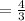
Now let us check to see if the two are parallel,


`(3)/( 4) \\eq (4)/(3)`
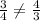
Since the two slopes are not the same, they are not parallel.


Now let us check to see if they are perpendicular


`(3)/(4) * (4)/(3) \\eq - 1`
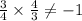
Since their product is not -1, the two lines are not perpendicular.

Hence ,

`y = (3)/(4) x + 12`
is neither parallel or perpendicular to

`y = (4)/(3) x - 2`

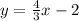
The next equation is


`y = - (4)/(3) x + 5`
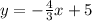
The slope of this equation is

`= - (4)/(3)`
Since,


`(3)/(4) * - (4)/(3) = - 1`

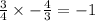
The equation

`y = (3)/(4) x + 12`
is perpendicular to


`y = - (4)/(3) x + 5`
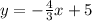
The next equation is


`y = (3)/(4) x`
Since the slope if the two are equal, that is


`(3)/(4) = (3)/(4)`
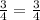
the two equations are parallel.





The next equation is


`y = - (4)/(3) x - 6`
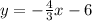
Since


`( 3)/(4) * ( - 4)/(3) = -1`
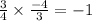
the two equations are perpendicular.


Question 5.

The given line in the graph passes through,

(10,7), (-8,-5) and (1,1).


Using any two points we can determine the slope,


`= (7 - - 5)/(10 - - 8)`

`= (7 +5 )/(10 + 8)`

`= (12)/(18) = (2)/(3)`


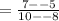
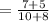
The line parallel to this line which passes through (5,-1), also has slope


`= (2)/(3)`
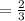
The equation of this line is


`y - - 1 = (2)/(3) (x - 5)`
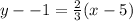
This implies that,


`y + 1 = (2)/(3) x - (10)/(3)`
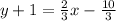
This simplifies to


`y = (2)/(3) x - (13)/(3)`

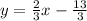
To find any point on this line, choose any value for x and solve the corresponding y value. So when

`x = 2`

`y = (2)/(3) * 2 - (13)/(3) = - 3`
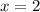
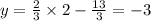
Hence


`(2 \: \: - 3)`
is a point on this line.