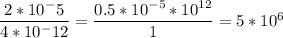Question

Estimate how many times larger 4 x 10^15 is than 8 x 10^9 in the form of a single digit times an integer power of 10.

Estimate how many times larger 2 x 10^-5 is than 4 x 10^-12 in the form of a single digit times an integer power of 10.

Answer 1

Problem A

When you use the term larger, you mean that (if the power is positive) the bigger number is in the numerator. 4*10^15 > 8 * 10^9 So 8 * 10^9 is in the denominator

Solution

`(4*10^(15))/(8*10^9) =0.5*10^6 =0.5*10^1*10^5=5*10^5`

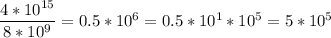
Note:The tricky part is recognizing what to do with the 0.5 * 10^6. You can always break apart a power into it's parts. Since 6 = 5 + 1, the power can be broken down into 10^1*10^5. The 10^1 is used to get the 0.5 to a number that is a single digit.

Problem 2

I'm just going to give you the answer to this. Please use Problem A as a guide.

`(2*10^-5)/(4*10^-12) = (0.5*10^(-5)*10^(12))/(1) = 5*10^6`