Question

Find b, if a is (5, -3) and m (-4, 2) is the midpoint of ab

Answer 1

We were given the points, A(5,-3) and the midpoint of AB, M(-4,2).

Let point B have coordinates (c , d).

Then the midpoint of A(5, -3) and B(c,d)



`= ( (5 + c)/(2) \: \: \: ( - 3 + d)/(2) )`
Now let us compare to the given midpoint M(-4, 2).

We can then write the following equations for the corresponding coordinates.

Comparing x coordinates, we have;


`( 5 + c)/(2) = - 4`
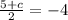
Multiplying both sides of the equation by 2 gives,

5+c = 2(-4)

Simplifying the right hand side gives,

5 + c = -8

Grouping like terms, we have,

c = -8 - 5

This simplifies to,
c = -13


Comparing y coordinates we have,


`( - 3 + d)/(2) = 2`
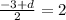
Multiplying through by 2 gives,

-3 + d = 2(2)

This means that,

-3 + d = 4

Making the subject we have,

d = 4+3

This implies that,

d = 7

Hence the coordinates of B are (-13,7).