Question

Which of the following is the solution to the compound inequality below? 3/2x+1/5≥-1 or -1/2 x-7/3≥ 5

Answer 1

For given relation the possible values for x can be given by

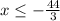`x\leq -(44)/(3)` or
`x> -(12)/(15)`

Explanation:

Given equations are

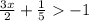`(3x)/(2)+(1)/(5)> -1` -------(A)

and
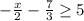`-(x)/(2)-(7)/(3)\geq 5` -------(B)

First consider equation (A)

`(3x)/(2)+(1)/(5)> -1 =>(3x)/(2)> -(6)/(5)`

=>
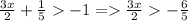
`x> -(12)/(15)` -------(C)

Now consider equation (B)

`-(x)/(2)-(7)/(3)\geq 5=>(x)/(2)\leq -(22)/(3)`

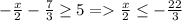
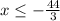`x\leq -(44)/(3)` ---------(D)

Using relation (C) and (D)

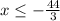`x\leq -(44)/(3)` or
`x> -(12)/(15)`

Thus for given relation the possible values for x can be given by

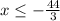`x\leq -(44)/(3)` or
`x> -(12)/(15)`

Answer 2

`(3)/(2)x + (1)/(5) \geq -1`

`(10)(3)/(2)x +(10) (1)/(5) \geq -1(10)`

15x + 2 ≥ -10

-2 -2

15x ≥ -12

`(15x)/(15) \geq (-12)/(15)`

x ≥
`(-12)/(15)`

x ≥
`(-4)/(5)`

OR

`-(1)/(2) x - (7)/(3) \geq 5`

`-(6)(1)/(2) x - (6)(7)/(3) \geq 5(6)`

-3x - 14 ≥ 30

+14 +14

-3x ≥ 44

`(-3x)/(-3) \leq (44)/(-3)`

`x \leq -(44)/(3)`

Graph: ←--------
`-(44)/(3)`
`(-4)/(5)` ----------→

Interval Notation: (-∞,
`-(44)/(3)]` U
`[(-4)/(5)`, ∞)