Question

Which of the following statements does not describe the altitude of a parallelogram?

Select all that apply.

It is the length of the parallelogram.
It is perpendicular to the base of the parallelogram.
It is the height of the parallelogram.
It connects opposite vertices of the parallelogram.
It is used in finding the area of a parallelogram.

Answer 1

It is the length of the parallelogram.

It connects opposite vertices of the parallelogram.

Explanation:

Refer the attached image.

We can see that it is not the length of a parallelogram, therefore the first statement does not describe the altitude of a parallelogram.

It is true that the perpendicular drawn from one of the vertices to the base of the parallelogram is the altitude of the parallelogram.

It is true that we also call it height of the parallelogram.

The line that connects the opposite vertices of the parallelogram is called diagonal not the height or altitude.

We use the height of the parallelogram to find the area of parallelogram.

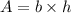`A = b* h`, where 'h' is the height of the parallelogram.

So, first and fourth statements does not describe the altitude of a parallelogram.