Hello!
Let's start off this problem by looking at what the standard form of a line, Ax + By = C, is, and the different aspects of it.
In the equation, A, B, and C are all constants and A is positive, while x and y are just left as such.
To find this equation however, from a given point and a given slope, you must first create another equation in a different form, and change it to that form. There is no way to find standard form, as of now, directly without using another equation (that I'm aware of).
There are two other types of equations (that are most commonly used, there are some others):
Point slope form: y -
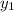 = m (x -
= m (x -
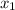 )
)
The y and x are left as such, m = slope, and
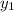 &
&
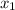 are the coordinates of any given point on the line.
are the coordinates of any given point on the line.
Things needed for this equation: slope and one point on the line
Slope Intercept form: y = mx + b
The m is the slope, and the b is the y intercept. The y and x are left as such. You can calculate b from a point on the line, but it's harder than just putting it in point slope form.
Things needed: slope, y intercept
As we can see, the form that would be the easiest to use is point-slope as it only needs a given point and slope, and we are provided that.
Now, for each question, I'm going to substitute in the values so it's in point slope form.
Here's the equation again: y -
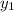 = m (x -
= m (x -
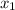 )
)
1. Given point: (-3, 2) Slope: 1
y - 2 = (x + 3)
2. Given point: (0, 5) Slope: -2
y - 5 = -2x
3. Given point: (4, 0) Slope: 5
y = 5 (x - 4)
Now, to convert into standard form, the only thing you need to do is distribute and then simplify.
As you have it in point slope form, the conversion is the last step. Distribute the slope to the values inside the parenthesis, and then multiply so all fractions become integers, and move the x and y to one side and the remaining number to the other.
1. y - 2 = x + 3
x - y = -5
2. y - 5 = -2x
2x + y = 5
3. y = 5 (x - 4)
y = 5x - 20
-5x + y = -20
A must be positive, so divide everything by -1.
5x - y = 20
Hope this helped!