Question

Find the rate of change and initial value. Y=mx+b

Answer 1

Y= 4/5 x + 24
To find the rate of change you find the difference in each of the numbers on the graph. For example, 36-32 is 4. So 28-4 is 24 and that would be the next number down. It would also match x to be 0 because since the rate of change for x was 5, if you subtract 5 from 5 you get 0. So from this we know that the coordinates would be 0,5.
From this info, the slope would be 4/5 and the y intercept or initial value would be 24

Answer 2

The rate of change (slope) (m) is
`(4)/(5)` .

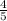The initial value (y-intercept) (b) is 24.

To find the rate of change (slope) and the initial value (y-intercept) for the given data points, we can use the formula for a linear equation in the form y=mx+b, where

m is the slope and

b is the y-intercept.

Let's use the given data points (5, 28) and (10, 32) to find the slope (m)

m=
`(change in y)/(change in x)`

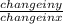
m=
`(32−28)/(10−5)`​ =
`(4)/(5)`

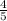
Now that we have the slope (m), we can use it along with one of the points (let's use (5, 28)) to find the y-intercept (b):

28=
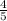`(4)/(5)` ×5+b

28=4+b

b=24

Therefore, the equation for the relationship between time and the number of cupcakes is y=
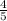`(4)/(5)`​ x+24.

In this equation:

The rate of change (slope) (m) is
`(4)/(5)` .

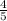The initial value (y-intercept) (b) is 24.