Question

If we assume that the metallic plates are perfect conductors, the electric field in their interiors must vanish. given that the electric field e⃗ due to a charged sheet with surface charge +σ is given by e=σ2ϵ0, and that it points away from the plane of the sheet, how can the condition that the electric field in plate i vanishes be written?

Answer 1

here the charge density of metal plate is given as

`charge density = \sigma`

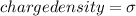
now the electric field is given Gauss law

`\int E. dA = (q)/(\epsilon_0)`

now here E = constant

so we will have

`E. \int dA = (q)/(\epsilon_0)`

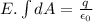
Since total area on both sides of plate will be double and becomes 2A

`E. 2A  = (q)/(\epsilon_0)`

`E = (q/A)/(2\epsilon_0)`

`E = (\sigma)/(2\epsilon_0)`

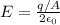
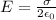
Now if we will find the electric field inside the metal plate

Then as we know that total charge inside the plate will always be zero

so we have

`E = 0`