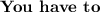
restrict the domains of quadratic functions and absolute value functions, because these functions are
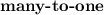
functions. For instance, the quadratic function f(x) = x^2 pairs both −2 and 2 with 4, and the absolute value function f(x) = |x| pairs both −2 and 2 with 2.
Linear functions (excluding constant functions) and exponential functions are
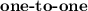
functions, so their domains
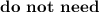
to be restricted.
_________________
An absolute value function, without domain restriction, has an inverse that is NOT a function.
In order to guarantee that the inverse must also be a function, we need to restrict the domain of the absolute value function to make it a one-to-one function.