Question

An adult human lung has a volume of 2.9 liters. If its volume decreases to 1.2 liters and it contains 0.049 mole of air after it exhales, how many moles of air does it contain when full?

A. 0.025 mol
B. 0.041 mol
C. 0.083 mol
D. 0.12 mol
E. 0.14 mol

Answer 1

D. 0.12

Step-by-step explanation

Answer 2

Answer:- The lung contains 0.12 moles of air when it's full.

Solution:- At constant temperature and pressure, the volume is directly proportional to the moles of the gas.

`(V_1)/(V_2)=(n_1)/(n_2)`

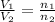
where,
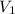`V_1` and
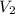`V_2` are the initial and final volumes. Similarly,
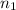`n_1` and
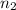`n_2` are the initial and final moles of the air.

Let's plug in the given values in the formula and solve this for initial moles of the gas.

`(2.9L)/(1.2L)=(n_1)/(0.049mol)`

`n_1=(2.9L(0.049mol))/(1.2L)`

`n_1=0.12mol`

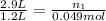
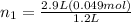
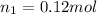
So, the lung contains 0.12 moles of air when it's full.