Question

A taxi service offers a ride with an $5 surcharge and charges $0.50 per mile. How many miles can a customer travel and spend at most $30? What linear inequality with variable x represents this situation? What is the solution to that inequality? Enter the solution as an inequality using x. Enter your answers in the boxes. Inequality: Solution:

Answer 1

Charges 0.50 per mile with a 5 dollar surcharge. Spending at most 30 dollars, the equation would be:

0.5x+5
`\leq`30

To find how many miles they can travel/the solution, solve the inequality:

`0.5x+5\leq30`

Subtract 5 from both sides.

`0.5x\leq25`

Divide both sides by 0.5.

`x\leq50`

They can travel (at most) 50 miles.

Hope this helps :)

Answer 2

Atmost 50 miles

`x\leq 50`

Explanation:

We are given that a taxi service offers a ride with 45 surcharge and charges $0.50 per mile.

We have to find how many miles can a customer travel and spent at most $30.

Charge of one mile=$0.50

Let x be the miles travel by customer

According to question

`0.50 x+5 \leq 30`

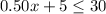
Subtracting 5 on both sides

`0.50 x+5-5\leq 30-5`

`0.50 x\leq 25`

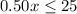
Divide by 0.50 on both sides

`x \leq (25)/(0.50)`

`x\leq 50`

Hence, the customer travel atmost 5 miles