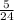Question

Starting at sea level, a submarine descends at a constant rate to a depth of −5/6 mile relative to sea level in 4 minutes. What was the submarine's depth relative to sea level after the first minute?

(NOTE: there are no answer choices)

Answer 1

I'm pretty sure it would be -5/24

Answer 2

Submarine's depth after first minute will be -
`(5)/(24)`

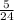
Explanation:

Submarine is descending at a constant rate = -
`(5)/(6)` miles in 4 minutes

Therefore, after the first minute submarine's depth relative to the sea level will be

=
`\frac{\text{Rate at which submarine is descending}}{\text{Time taken}}`

=
`-(5)/(6* 4)`

= -
`(5)/(24)`

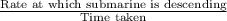
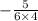
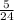
Therefore, submarine's depth after first minute will be -
`(5)/(24)`