Question

Calculati urmatoarele sume 1+2+3...+80. 2+4+6....+100. 1+3+5+...+99. 3+7+11+15+...+43

Answer 1

(a)

1+2+3+..........+80

we can see that this is arithematic sequence

so, first term is

`a_1=1`

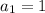
common difference is

`d=2-1`

`d=1`

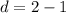
total term is

`n=80`

now, we can find sum of nth term

`S_n=(n)/(2)(2a_1+(n-1)d)`

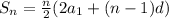
now, we can plug values

and we get

`S_8_0=(80)/(2)(2*1+(80-1)*1)`

`S_8_0=3240`...........Answer

(B)

2+4+6+.......+100

we can see that this is arithematic sequence

so, first term is

`a_1=2`

common difference is

`d=4-2`

`d=2`

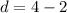
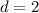
total term is

`a_n=a_1+(n-1)d`

`100=2+(n-1)*2`

`98=(n-1)*2`

`n=50`

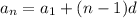
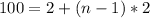
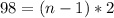
now, we can find sum of nth term

`S_n=(n)/(2)(2a_1+(n-1)d)`

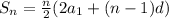
now, we can plug values

and we get

`S_5_0=(50)/(2)(2*2+(50-1)*2)`

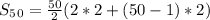
`S_5_0=2550`..........Answer

(C)

1+3+5+...+99

we can see that this is arithematic sequence

so, first term is

`a_1=1`

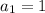
common difference is

`d=3-1`

`d=2`

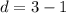
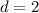
total term is

`a_n=a_1+(n-1)d`

`99=1+(n-1)*2`

`98=(n-1)*2`

`n=50`

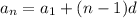
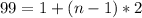
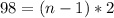
now, we can find sum of nth term

`S_n=(n)/(2)(2a_1+(n-1)d)`

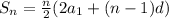
now, we can plug values

and we get

`S_5_0=(50)/(2)(2*1+(50-1)*2)`

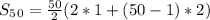
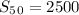`S_5_0=2500`..........Answer

(D)

3+7+11+15+...+43

we can see that this is arithematic sequence

so, first term is

`a_1=3`

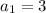
common difference is

`d=7-3`

`d=4`

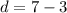
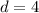
total term is

`a_n=a_1+(n-1)d`

`43=3+(n-1)*4`

`40=(n-1)*4`

`n=11`

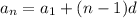
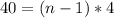
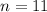
now, we can find sum of nth term

`S_n=(n)/(2)(2a_1+(n-1)d)`

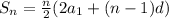
now, we can plug values

and we get

`S_1_1=(11)/(2)(2*3+(11-1)*4)`

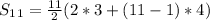
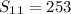`S_1_1=253`..........Answer