Question

Barneys money earned $204 in interest after 1 year. He invested some of his money in an account earning 6% simple interest and $405 more than that amount in an account earning 5% simple interest. Find the amount Barney invested in each account ? plz show work ..

Answer 1

Let P be the principal.

SI from the first account =
`(PNR)/(100)`

`=(x(1)(6))/(100)`

`=(6x)/(100)`

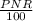
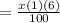
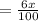
SI from the second account =
`((x+405)(1)(5))/(100)`

`=(5(x+405))/(100)`

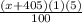
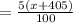
Total money earned in interest after 1 year = $204.

Therefore,
`(6x)/(100) +(5(x+405))/(100) =204`

`(6x+5x+2025)/(100) = 204`

`(11x+2025)/(100) =204`

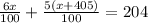
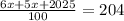
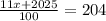
11x + 2025 = 20400

11x = 20400 - 2025

11x = 18375

x = 18375/11

x = 1670.45

x + 405 = 1670.45 + 405 = 2075.45

Hence, Barneys investment in the first account is $1670.45 and her investment in the second account is $2075.45.