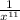Question

Simplify without negative exponents x^-4/x^7

Answer 1

I'm going to take your x^-4/x^7 and rewrite it for greater clarity:

x^(-4)

---------

x^7

If we now mult. both the numerator and the denom. of this expression by x^4, we obtain:

1

--------

x^13

which is equivalent to the given expression but without a negative exponent.

Answer 2

Answer: The answer to the given expression is
`(1)/(x^(11))`

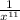
Explanation:

We are given an expression:
`(x^(-4))/(x^7)`

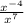
To simplify this, we use the laws of exponents:

1. 
   `(x^m)/(x^n)=x^(m-n)`
2. 
   `x^(-m)=(1)/(x^m)`

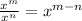
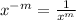
Simplifying the expression using law 1, we get:

`\Rightarrow (x^(-4))/(x^7)=x^(-4-7)=x^(-11)`

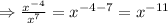
Now, using law 2, we get:

`\Rightarrow x^(-11)=(1)/(x^(11))`

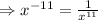
Hence, the answer to the given expression is
`(1)/(x^(11))`