Question

Line g passes through points (1, 1) and (10, 9). Line h is perpendicular to g. What is the

slope of line h?

Answer 1

`\bold{The~slope~of~line~h~is~-(9)/(8). }`

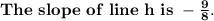
Explanation:

Hi there!

First, let's calculate the slope of line g.

`\displaystyle(y2-y1)/(x2-x1)`

`\displaystyle(9-1)/(10-1) \\ \displaystyle(8)/(9)`

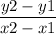
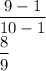
So, the slope of line g is
`\displaystyle(8)/(9)`

Now let's identify the slope of line h.

We are given that line h is perpendicular to line g.

Now, perpendicular lines have slopes that are opposite reciprocals.

This means we take a number, flop it over, and change its sign.

The slope of line g is

`\displaystyle(8)/(9)`

Now, we flop it over:

`\displaystyle(9)/(8)`

Then, we change its sign:

`\displaystyle-(9)/(8)`

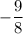
Thus,
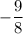`\displaystyle-(9)/(8)` is our final answer.

Hope it helps! Enjoy your day! (:

`\bold{GazingAtTheStars}`