Question

Juan tiene cubos azules de 55 mm de arista y cubos rojos de 45 mm de arista. Los apila en dos columnas, una de cada color ; quiere conseguir que las dos columnas sean igual de altas. ¿cuántos cubos necesita,como mínimo, de cada color?

Answer 1

the question in English

Juan has blue cubes with a 55 mm edge and red cubes with a 45 mm edge. He stacks them in two columns, one of each color; he wants the two columns to be the same height. How many cubes does he need, as a minimum, of each color?

Let

x---------> the number of blue cubes

y--------> the number of red cubes

we know that

Juan wants that the two columns to be the same height

so

`55x=45y`

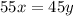
solve for y

`y=(55)/(45)x`

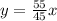
I proceed to calculate a table, assuming values of x to calculate the value of y. When the values of x and y are whole numbers, I will have found the solution.

the table in the attached figure

therefore

the answer is

9 blue cubes

11 red cubes