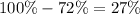Question

If the probability of rain today is 72%, what is the probability that it will not rain today?

Answer 1

The probability of any event is a number ranging from 0 to 1.

Once you partition the sample space (i.e. you find a sequence of events which are disjointed and cover the whole sample space), you know that the sum of the probabilities of the events in the partition is 1.

In particular, for every event
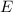`E`, the event and its negation
`\lnot E` are a partition: they are disjointed (it is impossible that both an event and its negation happen at the same time) and they cover the whole sample space (the event will either happen or not happen, there are no alternatives).

So, you know that

`P(E) + P(\lnot E) = 1`

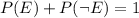
And you can deduce that

`P(\lnot E) = 1-P(E)`

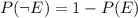
This is a fundamental equation in probability: the probability of the negation of an event is the complementary to 1 of the probability of that event.

When dealing with percentage, 1 means 100%. So, if it rains with probability 72%, it doesn't rain with probability

`100\%-72\% = 27\%`

Answer 2

will rain + will not rain = 100%

72% + will not rain = 100%

will not rain = 28% subtracted 72% from both sides

Answer: 28%