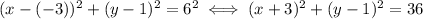Question

A circle with centre (-3, 1) passes through the point (3, 1).find the equation

Answer 1

The general formula for a circle with center (a,b) and radius r is

`(x-a)^2 + (y-b)^2 = r^2`

If we know the center and a point on the circle, the squared radius is given by substituting in the point for x and y.

`(x - -3)^2 + (y - 1)^2 = (3 - -3)^2 + (1 - 1)^2`

Answer:

`(x+3)^2 + (y-1)^2 = 36`

Answer 2

To write the equation of a circle, you need its radius and its center. The center is given, and you can easily derive the radius: it is the distance between the center and any point in the circumference.

In your case, the center is
`(-3,1)`, and the point on the circumference is
`(3,1)`. These points are 6 units apart, so the radius is 6.

Now, knowing the center
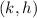`(k,h)` and the radius
`r`, the equation is

`(x-k)^2+(y-h)^2 = r^2`

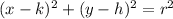
Plugging your values, you have

`(x-(-3))^2+(y-1)^2 = 6^2 \iff (x+3)^2+(y-1)^2 = 36`