The distance between P and R is equal to the net displacement of the ship in going from port P to port R
Vector P = 30 km North
Vector R = 20 km 30° east of north
Now, the angle between Vector P and vector R = 90° + 30 ° = 120°
Using the formula to find the addition of two vectors:
Resultant =

Plugging the values:
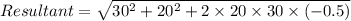
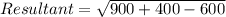
Resultant = 26.457 Km
The distance from P to R is 26.457 km