The answer is B.
The absolute value is the "positive version" of a number. So, the absolute value does nothing to positive numbers, and switches the sign of negative numbers. Here are some examples:
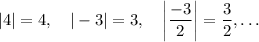
So, as you can see, the result of an absolute value can't be negative, and as such, it can't be less than a negative number.