Question

You are an engineer in charge of designing a new generation of elevators for a prospective upgrade to the Empire State Building. Before the state legislature votes on funding for the project, they would like you to prepare a report on the benefits of upgrading the elevators. One of the numbers that they have requested is the time it will take the elevator to go from the ground floor to the 102nd floor observatory. They are unlikely to approve the project unless the new elevators make the trip much faster than the old elevators.

If state law mandates that elevators cannot accelerate more than 2.70 m/s2 or travel faster than 14.3 m/s , what is the minimum time in which an elevator can travel the 373 m from the ground floor to the observatory floor?

Answer 1

31.38 s (2 d.p.)

Step-by-step explanation:

Constant Acceleration Equations (SUVAT)

`\boxed{\begin{array}{c}\begin{aligned}v&=u+at\\\\s&=ut+(1)/(2)at^2\\\\ s&=\left((u+v)/(2)\right)t\\\\v^2&=u^2+2as\\\\s&=vt-(1)/(2)at^2\end{aligned}\end{array}} \quad \boxed{\begin{minipage}{4.6 cm}$s$ = displacement in m\\\\$u$ = initial velocity in ms$^(-1)$\\\\$v$ = final velocity in ms$^(-1)$\\\\$a$ = acceleration in ms$^(-2)$\\\\$t$ = time in s (seconds)\end{minipage}}`

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.

-----------------------------------------------------------------------------

To find the minimum time in which an elevator can travel the 373 m from the ground floor to the observatory floor, we to accelerate to the maximum allowed velocity as quickly as possible, maintain the maximum velocity for as long as possible, and then decelerate for the shortest period of time in order for the elevator to come to a stop after 373 m.

Therefore, the travel time from the start of the elevator trip to the end will have three phases:

• Acceleration
• Constant velocity
• Deceleration

Phase 1 - Acceleration

Given information:

• 
  `u = 0 \sf \; m/s`
• 
  `v= 14.3 \sf \; m/s`
• 
  `a= 2.70 \sf \; m/s^2`

The time it takes to accelerate from rest to the maximum allowed velocity, where the elevator accelerates at the maximum allowed acceleration:

`\begin{aligned}v & = u+at\\\implies 14.3 & = 0+2.7t\\t & = (14.3)/(2.7)\\t & = 5.296296296\;\sf s\end{aligned}`

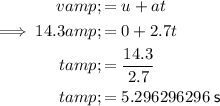
The distance covered in this time is:

`\begin{aligned}v^2 & = u^2 + 2as\\\implies 14.3^2 & = 0^2 + 2(2.7)s\\204.49 & =5.4s\\s & = (204.49)/(5.4)\\s & = 37.86851852\; \sf m\end{aligned}`

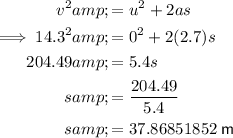
Phase 3 - Deceleration

Given information:

• 
  `u = 14.3 \sf \; m/s`
• 
  `v= 0 \sf \; m/s`
• 
  `a= -2.70 \sf \; m/s^2`

When the elevator is decelerating from the maximum velocity to being at rest, it will take the same amount of time and cover the same distance as its acceleration phase:

`\begin{aligned}v & = u+at\\\implies 0& = 14.3+(-2.7)t\\2.7t&=14.3\\t & = (14.3)/(2.7)\\t & = 5.296296296\;\sf s\end{aligned}`

`\begin{aligned}v^2 & = u^2 + 2as\\\implies 0^2 & = 14.3^2 + 2(-2.7)s\\0 & = 204.49 -5.4s\\5.4s&=204.49\\s & = (204.49)/(5.4)\\s & = 37.86851852\; \sf m\end{aligned}`

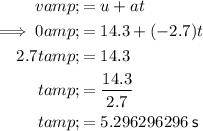
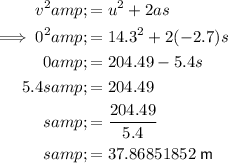
Phase 2 - constant velocity

The total distance the elevator travels is 373 m.

Therefore, the distance it travels during phase 2 when it is traveling at a constant (maximum) velocity is the total distance less the distance traveled in phases 1 and 3:

`\begin{aligned}\implies s & =373-2(37.86851852)\\s& = 297.262963\;\sf m\end{aligned}`

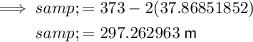
Given information:

• 
  `u = 14.3 \sf \; m/s`
• 
  `v= 14.3 \sf \; m/s`
• 
  `s = 297.262963\;\sf m`

Therefore, the time is takes to travel this distance when it is traveling at a constant (maximum) velocity is:

`\begin{aligned}s&=\left((u+v)/(2)\right)t\\\implies 297.262963 & = \left((14.3+14.3)/(2)\right)t\\297.262963 & = 14.3t\\t & = (297.262963)/(14.3)\\t & = 20.78761979 \; \sf s\\\end{aligned}`

Total minimum time

Therefore, the minimum time is the sum of the time calculated for the three phases:

`\begin{aligned}\sf Minimum \: time& = \sf Phase \: 1 + Phase \: 2 + Phase \: 3\\& = 5.296296...+5.296296...+20.78761...\\& = 31.38021...\\& = 31.38\; \sf s\end{aligned}`