The given formula for the perimeter of a rectangle is given by the equation as:
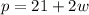
we have to determine the equivalent equation, which is used to solve for the variable 'w'.
Since,
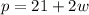
Subtracting '21' from both the sides of the given equation, we get
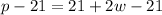
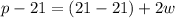
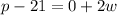
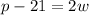
Dividing by '2' from both the sides of the equation, we get as
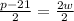
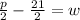 is the required equation used to solve for the variable 'w'.
is the required equation used to solve for the variable 'w'.