Question

You have 250,000 In an IRA at the time you retire.You have the option of investing this money in two funds.Fund A pays 1.2% annually and Fund B pays 6.2% annually.How should you divide your money between Fund A and Fund B to produce and annual interest income of $8,000?

Answer 1

Let x be the amount of money, you fund in Fund A and y be the amount of mone yyou fund in Fund B.

1. You have 250,000 In an IRA at the time you retire and want to invest this money into Funds A and B, then

`x+y=250,000.`

2. Fund A pays 1.2% (as a decimal 1.2% is 0.012) annually, then
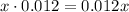`x\cdot 0.012=0.012x` is annual interest income in Fund A.

Fund B pays 6.2% (as a decimal 6.2% is 0.062) annually, then
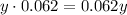`y\cdot 0.062=0.062y` is annual interest income in Fund B.

Since Fund A and Fund B produce an annual interest income of $8,000, then

`0.012x+0.062y=8,000.`

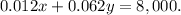
3. Solve the system of equations:

`\left\{\begin{array}{l}x+y=250,000\\0.012x+0.062y=8,000.\end{array}\right.`

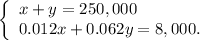
Express x from first equation
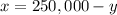`x=250,000-y` and substitute it into the second equation

`0.012(250,000-y)+0.062y=8,000.`

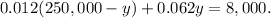
Multiply this equation by 1000:

`12(250,000-y)+62y=8000,000,\\ \\3000,000-12y+62y=8000,000,\\ \\62y-12y=8000,000-3000,000,\\ \\50y=5000,000,\\ \\y=100,000`

Then

`x=250,000-100,000=150,000.`

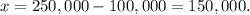
Answer: you have to fund $150,000 in Fund A and $100,000 in Fund B.