volume of the box is 675 cubic inches
A machine produces open boxes using square sheets of plastic.
It is a square sheet so length and width are same
Lets assume length as x so width is also x
The machine cuts equal-sized squares measuring 3 inches on a side from each corner of the sheet.
After turning up the sides the height of the box becomes 3 inches
We know the volume of a box formula
Volume = Length * width * height
We know length is x , width is x and height = 3
So V = x * x * 3
Given volume = 675 cubic inches
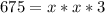
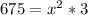
Divide by 3 on both sides
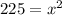
Now we take square root on both sides
x = 15
the length of one side of the open box is 15 inches.