Question

Matt is canoeing on Lake opeongo fighting a headwind. it takes him 2 hours to get to the lake 4km away. on the way back it takes him 90 minutes. how fast can he canoe without wind? How much is the wind slowing him down

Answer 1

So Matt is canoeing on a Lake.

It took him 2 hours to get to the lake 4 kilometers away.

On the way back it takes him 90 minutes.

Now, lets say that he is canoeing at 'u' miles per hour and lets assume that the speed of the wind is 'v' miles per hour.

While he sails in opposite to the wind net speed is given by
`u-v`.

Using the relation between distance, time, and speed we get:

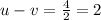`u-v=(4)/(2) =2` kilometers per hour so we get,

`u-v=2` ..............(equation 1)

Now when he sails along the wind, the net speed is given by
`u+v`

Now, again use the same relation as stated above we get:

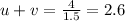`u+v=(4)/(1.5) =2.6` (here we have converted 90 minutes into hours
`(90)/(60) =1.5`)

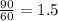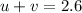`u+v=2.6` ..............(equation 2)

Solving equation 1 and 2 we get:

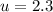`u=2.3` , putting the value of 'u' in equation 1 we get
`v=2.6-2.3=0.3`.

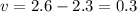So the speed at which Matt is canoeing is 'u' that is 2.3 kilometers per hour and the wind is flowing at 0.3 kilometers per hour.

So Matt can canoe at 2.3 kilometers per hour without wind. And wind is slowing him down by 0.3 kilometer per hour.