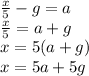So basically everything we do is an inverse operation. Like Subtraction undoes Addition and Addition undoes Subtract.
Division undoes Multiplication and Multiplication undoes Division.
You see a over b is being divided, so to undo division we need to multiply by the reciprocal of the a/b or whatever the fraction you have in a equation. The reciprocal of a/b is b/a, however knowing that we don't need all that fancy math language, we now KNOW TO JUST MULTIPLY THE DENOMINATOR TO BOTH SIDES OF THE EQUAL SIGN, LIKE THIS
13. More Work Shown - Solving For b
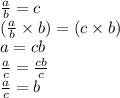
14. Less Work Shown - Solving For J
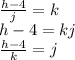
15. Less Work Shown - Solving For X