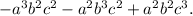Question

Find the product.

-a ^2 b ^2 c^ 2(a + b - c)

Answer 1

Answer: The required product is
`-a^3b^2c^2-a^2b^3c^2+a^2b^2c^3.`

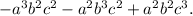
Step-by-step explanation: We are given to find the following product :

`P=-a^2b^2c^2(a+b-c)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

To find the given product, we must multiply the first common term to each term within the bracket.

The evaluation of the product (i) is as follows :

`P\\\\=-a^2b^2c^2(a+b-c)\\\\=-a^2b^2c^2* a-a^2b^2c^2* b+a^2b^2c^2* c\\\\=-a^3b^2c^2-a^2b^3c^2+a^2b^2c^3.`

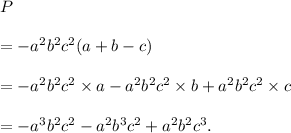
Thus, the required product is
`-a^3b^2c^2-a^2b^3c^2+a^2b^2c^3.`

Answer 2

`\text{Use distributive property:}\\a(b + c) = ab + ac\\\\and\ a^n\cdot a^m=a^(n+m)`

`-a^2b^2c^2(a+b-c)=(-a^2b^2c^2)(a)+(-a^2b^2c^2)(b)+(-a^2b^2c^2)(-c)\\\\=-a^3b^2c^2-a^2b^3c^2+a^2b^2c^3`