Question

A ghost on a 135 feet cliff perpendicular (at 90 degrees) to the ground looks down at an angle of 16 degrees and sees a

werewolf. How far away is the ghost from the werewolf approximately? How far away is the wolf from the base of the cliff? Sketch the
triangle that matches this scenario with a ruler and protractor, and use this diagram and scales to solve for these distances between
the ghost, wolf and cliff. Explain how you got your answer.

Answer 1

To solve this problem you must apply the proccedure shown below:

1. You can make the diagram attached, where the ghost is identified as G and the the werewolf as W. The distance between both of them is y and the distance of the werewolf from the base of the cliff is x.

2. Let's calculate y:

`Cos(16)=(135)/(y)`

`y=(135)/(Cos(16))`

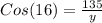
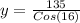
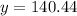`y=140.44` ft

3. Now, let's calculate x:

`Tan(16)=(x)/(135)`

`x=(135)(Tan(16))`

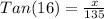
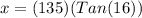
`x=38.71` ft

The answer are:

• The ghost is 140.44 feet from the werewolf.
• The werewolf is 38.71 feet from the base of the cliff.