Given
∆PQR points are P(-2,5), Q(-1,1), and R(7,3)
Determine whether ∆PQR is a right triangle
To proof
As given ∆PQR points are P(-2,5), Q(-1,1), and R(7,3)
First find out the sides of triangle
FORMULA
Distance formula between two points
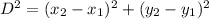
Distance between two points P(-2,5) and Q(-1,1)

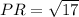
Distance between two points Q(-1,1)and R(7,3)
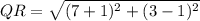
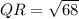
Distance between two points R(7,3) and P(-2,5)
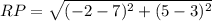
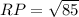
now show that ∆PQR is a right triangle
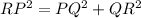
Putting the value given above
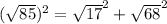
85 = 17 +68
85 =85
In the right triangle
HYPOTENUSE² = BASE² + PERPENDICULAR²
This is prove above
Hence ∆PQR is a right triangle
Hence proved