Question

Let h(x)=g∘ f)(x)=1/(x+3)^2

which of the following could be a possible decomposition of h(x)

f(x)=x^2; g(x)=x+3
f(x)=1/x; g(x)=x+3
f(x)=x+3;g(x)=1/x^2
f(x)=1/x^2;g(x)=x+3

Answer 1

Since,
`h(x)= (g \circ f)(x)= (1)/((x+3)^2)`,

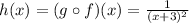We have to determine the possible decomposition of h(x).

1. Consider
`f(x)=x^2, g(x)=x+3`

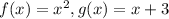
`(g\circ f)(x) = g(f(x))=g(x^2)=x^2+3` which is not equal to the given h(x). This option is not correct.

2. Consider
`f(x) = (1)/(x) , g(x)=x+3`

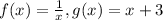
`(g\circ f)(x) = g(f(x))=g((1)/(x))=(1)/(x)+3 =(1+3x)/(x)` which is not equal to the given h(x). This option is not correct.

3. Consider
`f(x)= x+3 , g(x)= (1)/(x^2)`

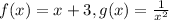
`(g\circ f)(x) = g(f(x))=g((x+3))= (1)/((x+3)^2)` which is equal to the given h(x). This option is correct.

So, the correct decomposition of h(x) are f(x) = (x+3) and g(x)=
`(1)/(x^2)`.

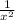Therefore, Option 3 is the correct option.