The equation of a circle:
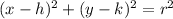
(h, k) - center
r - radius
We have the points A(-1, 7) and B(7, 7). AB is a diameter of a circle.
The midpoint of diameter is a center of a circle.
Calculate this using:
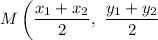
Substitute
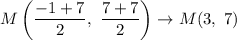
Therefore we have h = 3 and k = 7.
Calculate a length of a radius using:
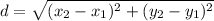
Substitute coordinates of the points (3, 7) and (7, 7):
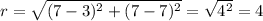
Your answer is:
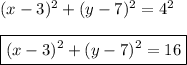
------------------------------------------------------------------------------------------
You can read the coordinates of the center and length of a radius from a graph.
Look at the picture.