Question

The coordinates of the vertices of ∆PQR are P(-2,5), Q(-1,1), and R(7,3). Determine whether ∆PQR is a right triangle. Show your work and explain your answer!

Answer 1

Solution: Yes, triangle PQR is a right angle triangle.

Step-by-step explanation:

It is given that P(-2,5), Q(-1,1) and R(7,3).

Distance between two points
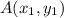`A(x_1,y_1)` and
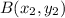`B(x_2,y_2)` is given by he formula,

`AB=√((x_2-x_1)^2+(y_2-y_1)^2)`

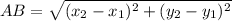
Use this formula to find the length of sides.

`PQ=√((1)^2+(-4)^2) =√(17)`

`QR=√((8)^2+(2)^2) =√(68)`

`PR=√((9)^2+(-2)^2) =√(85)`

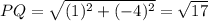
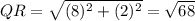
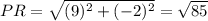
By pythagoras theorem a triangle is a right angle triangle if and only if the sum of squares of two small sides is equal to the square of the largest side.

Since the greatest side is PR.

`(PQ)^2+(QR)^2=(√(17))^2+(√(68))^2 \\(PQ)^2+(QR)^2=17+68\\(PQ)^2+(QR)^2=85\\(PQ)^2+(QR)^2=(PR)^2`

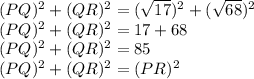
Hence, the triangle PQR is a right angle triangle.