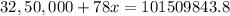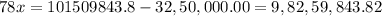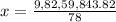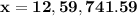Question

Northwestern energy estimates that the present worth now of income from an investment in renewable energy sources is $12,475,000. There will be no income in years 1 and 2, but in year 3 income will be $250,000, and thereafter it will increase linearly through year 15. What is the required gradient of income growth, if interest rate is 15% per year?

Answer 1

Answer: The gradient of income growth is $12,59,741.59. This means that income must rise by $12,59,741.59 each year.

We follow these steps to arrive at the answer:

1. Calculating the total value of earnings after 15 years

We calculate the Future Value of the investment as follows:

`\mathbf{FV = PV * (1+r)^(n)}`

`FV = 12475000 * (1+0.15)^(15)`

`\mathbf{FV = 101509843.8}`

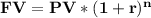
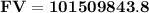
This represents the total of revenues earned over 15 years from the investment.

2.Calculating the gradient

Since income increases linearly over 15 years, we can consider year 3 earnings as the base. Let the income increase in year 4 by x. Since income increases yearly, we can calculate income in each year as follows

Year Revenues

1 0

2 0

3 250000

4 250000 + x

5 250000 + 2x

6 250000 + 3x

7 250000 +4x

8 250000 + 5x

9 250000 + 6x

10 250000 + 7x

11 250000 + 8x

12 250000 + 9x

13 250000 + 10x

14 250000 + 11x

15 250000 + 12x

Total 32,50,000.00 + 78x

Now we equate the values in steps 1 and above to find 'x' the gradient

`32,50,000 + 78x = 101509843.8\\`

`78x = 101509843.8 - 32,50,000.00 = 9,82,59,843.82`

`x = (9,82,59,843.82)/(78)`

`\mathbf{x = 12,59,741.59}`