You're using Rolle's theorem. This theorem states that, if a function is continous in
![[a,b]](https://img.qammunity.org/2019/formulas/mathematics/high-school/hycs8sttkhnuq5yfuhyfhr31suzra3n6sc.png) and differentiable in
and differentiable in
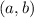 , and
, and
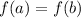 , then there exists a middle point
, then there exists a middle point
![c \in [a,b]](https://img.qammunity.org/2019/formulas/mathematics/high-school/ie78v1s275i4689rdkizaieukroeretbtt.png) such that
such that
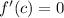
In other words, if a continous and differentiable function starts and ends at the same height, then it has a maximum or minimum.
In your case, since the function is differentiable in the closed interval, it is also continuous in the closed interval (differentiability implies continuity), and also being differentiable in the closed interval obviously implies that the function is differentiable in the open interval. Also, you're given that the function evaluates to 4 at both extreme points, so the hypothesis of the theorem are granted.