Question

Jim has a total of 77 red and blue marbles. The number of blue marbles is five more than twice the number of red marbles.

Answer 1

Explanation:

r + 2r+5 = 77

3r = 72

red = 24 (# of red marbles)

----------------

Solve for "b"::

b = 77 - r = 77-24 = 53 (# of blue marbles)

--------------

Cheers,

Stan H.

Answer 2

Let r and b represent, respectively, the number of red and blue marbles. We know a couple of things:

• The total number of marbles is 77, so
  `r+b = 77`
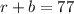
• The number of blue marbles is five more than twice the number of red marbles, so
  `b = 2r+5`

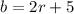
So, we have the following system:

`\begin{cases} r+b = 77\\b = 2r+5\end{cases}`

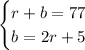
The second equation gives a way to express b in terms of r. Use this expression in the first equation:

`r+b = 77 \iff r+(2r+5)=77 \iff 3r+5=77 \iff 3r = 72 \iff r = 24`

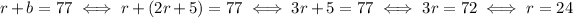
So, if Jim has 24 red marbles, he has
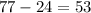`77-24 = 53` blue marbles.